Sobrevivencia en el Titanic, parte 2

Este post presenta un análisis la base Titanic usando un modelo aditivo generalizado logístico.

Los modelos aditivos generalizados (GAMs) relacionan forma no lineal al conjunto de v.a. independientes Z = \{Z_1,Z_2,\ldots,Z_n\}, tal que Z_i = (Y_i,X_i) \in \mathbb R^{d+1}. La colección Z sigue un GAM si:

Y_i \sim \mathscr{F}_\varepsilon (\theta_i), \quad \text{y } g(\theta_i) = \sum_{s = 1}^mf_s(X_i), Donde:

• \mathscr{F}_\varepsilon representa la familia exponencial.

• El conjunto \theta = \{\theta_i\} representa una colección de parámetros de locación.

• g: \mathbb R \to \mathbb R es una función diferenciable e invertible, conocida como la función de enlace.

• \beta \in \mathbb R^{d+1} es el vector de coeficientes de regresión o importancias.

• las funciones f_s:\mathbb{R}^d \to \mathbb R son suaves y diferenciables, de tal forma que, se pueden aproximar mediante la siguiente expresión:

f_s(X) \approx \sum^K_{k = 1}\beta_{k,s} b_{k,s}(X),

• donde \beta_{k,s} son los coeficientes por estimar y b_{k,s}(X) son una base de funciones “conocidas.”

Dado que
B_s(X) = [b_{1,s}(X),b_{2,s}(X),\ldots,b_{K,s}(X)], es una base, entonces los b_{k,s}(X) son una colección linealmente independiente en un espacio de funciones (L_2). Este resultado implica que estimar la función no lineal f_s(X) es equivalente a resolver el problema de regresión lineal:

\hat f_s(X) = B_s(X) \hat \beta. Este tipo de modelos tiene dos limitantes, el primero es seleccionar una base adecuada, y segundo elegir el número de óptimo de elementos en la base K. Si K es muy grande el modelo sobre-ajusta los datos (overfitting). Una solución es penalizar el suavizado con:

P(f) = \int \partial^2f^2(x) dx. Por lo tanto, el problema de optimización se escribe como:

\hat \beta_s = \arg \min_\beta ||g^{-1}(y) - f_s(X)||^2 + \lambda P(f), \hat \beta_s = \arg \min_\beta || g^{-1}(y) - B_s(X)\beta ||^2 + \lambda \beta^tS\beta.

Donde S = \int B_s^t(X)B_s(X) dx, es la penalización. Note que el problema de optimización anterior es equivalente a resolver un problema de regresión lineal penalizado, que a su vez puede ser re-escrito como un problema de regresión lineal completo.

Ejemplo: mcycle dataset

Code

library(mgcv)
library(caret)
library(tidymv)
library(GGally)
library(ggplot2)
library(flextable)
library(bayesplot)

bayesplot_theme_set(theme_grey())
data("mcycle",package = "MASS")
load("Titanic.RData")

La base de datos mcycles presenta una serie de mediciones de la aceleración de cabezas en un accidente motorizado simulado para probar la resistencia al impacto en cascos. La base de datos contiene las siguiente variables:

• accel: La aceleración obtenida al momento de impacto. (Dependiente)

• times: El tiempo previo al impacto. (ms)

ggplot(mcycle,aes(times, accel))+
  geom_point()+
  labs(title = "Aceleración de cabezas al momento de impacto",
       subtitle = "Accidentes motorizados simulados",
       y = "aceleracion (g)",x  = "tiempo (ms)")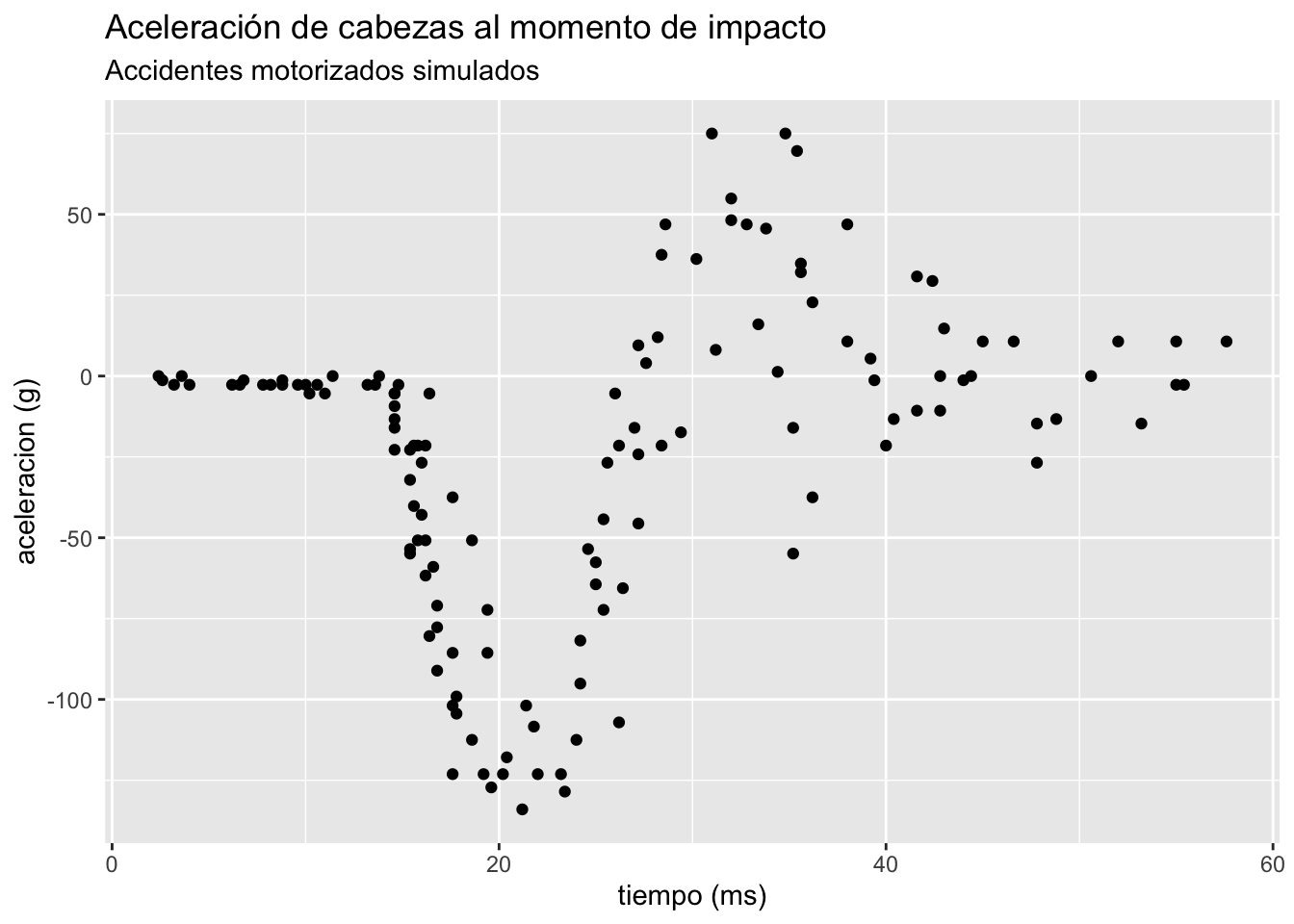

Figure 1: Gráfico de dispersión de las simulaciones.

Para medir la relación de la aceleración obtenida de los accidentes utilizaremos un GAM normal tal que:

accel_i \sim N(\mu_i,\sigma^2), \quad g(\mu_i) = \mu_i, \text{ y } \mu_i = f(times_i). Donde f(times) = \sum^k_{t = 1}\beta_t b_t(times) representa aproximación por base Splines para la media del modelo. El siguiente código limpia la base de datos para obtener las variables de interés

m1 = gam(accel ~ s(times,k = 15,bs = "fs",m = 2),data = mcycle)
summary(m1)

Family: gaussian 
Link function: identity 

Formula:
accel ~ s(times, k = 15, bs = "fs", m = 2)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -25.546      1.965     -13   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
           edf Ref.df     F p-value    
s(times) 10.44  12.18 38.07  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =   0.78   Deviance explained = 79.8%
GCV = 561.61  Scale est. = 513.3     n = 133

El resumen del modelo presenta un análisis de significancia para el vector de parámetros \hat \beta, que en este caso es de dimensión d = 15, y que debido al TLC se distribuye normal multivariada. El siguiente código genera una muestra Bootstrap para cada uno de los parámetros del modelo M_1.

Code

gam_boots = function(dat,B = 2000){
  n = dim(dat)[1]
  est = NULL
  for (i in 1:B) {
    si = sample(x = 1:n,size = n,replace = TRUE)
    mli = gam(accel[si] ~ s(times[si],k = 15,bs = "fs",m = 2),data = dat)
    ci = as.array(mli$coefficients)
    est = rbind(est,ci)
  }
    # Estética
  cn = dim(est)[2]-1
  colnames(est) = c("intercepto",paste0("beta",1:cn))
  return(est)
}

Obtenemos una muestra Bootstrap para los estimadores \hat \beta de tamaño B = 2,000 repeticiones.

btp = gam_boots(dat = mcycle,B = 2000)

color_scheme_set("viridis")

mcmc_dens(btp)+
  labs(title = "Distribución muestral de los estimadores, GAM",
       subtitle ="Bootstrap B = 2,000 iteraciones")

Figure 2: Gráfico de densidades. Cada densidad representa la distribución muestral aproximada para cada uno de los estimadores usando un Bootstrap de B = 2,000 iteraciones.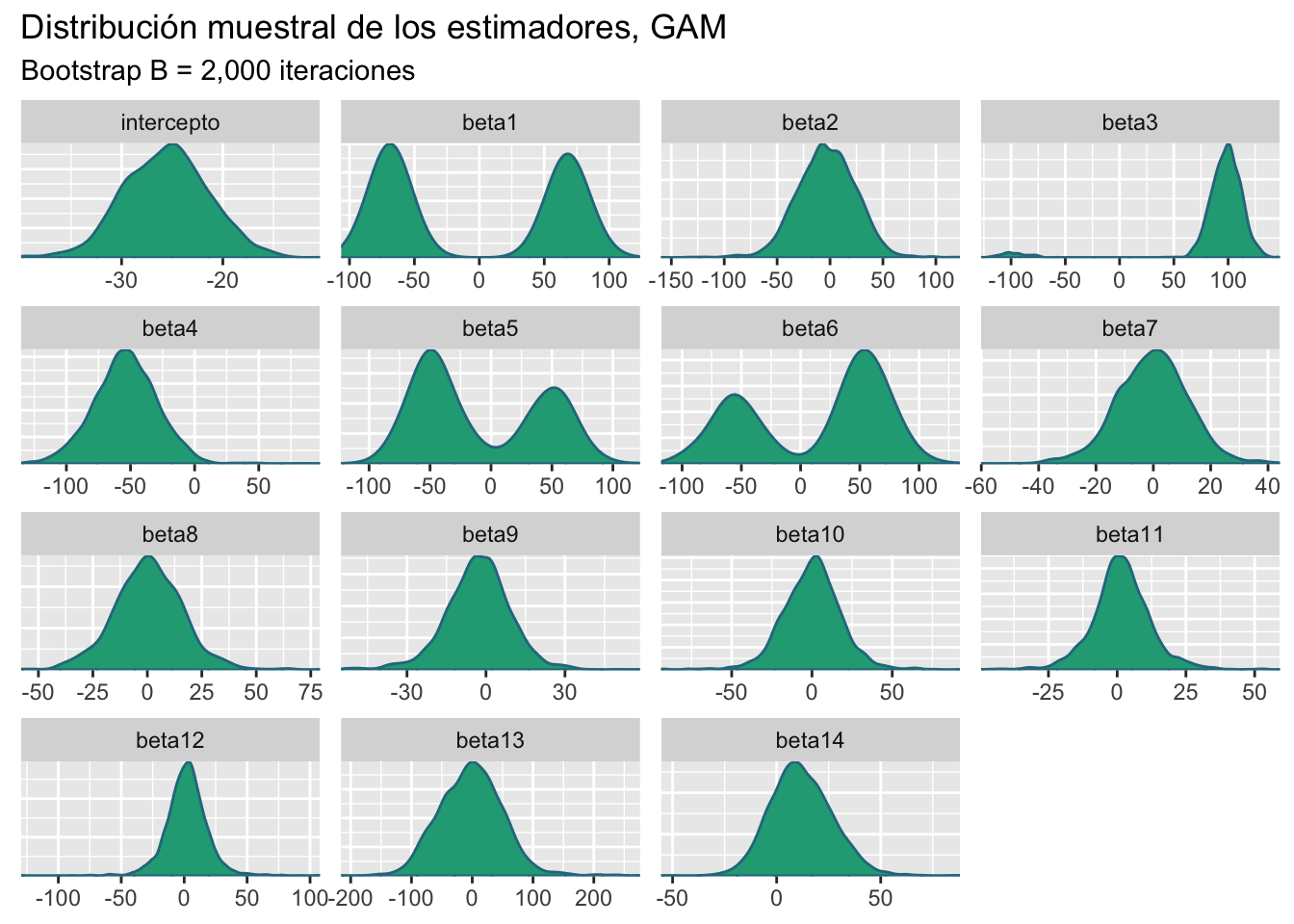

Los intervalos de confianza al 95% son:

x = apply(btp,MARGIN = 2, FUN = quantile, probs = c(0.025,0.5,0.975)) 

# Estética
x = data.frame( t(x) )
x$pars = c("intercepto",paste0("beta",1:14))
colnames(x) = c("q2.5%","Median","q97.5%","parámetros")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 1: Intervalos de confianza al 95%, obtenidos a partir de una muestra bootstrap de B = 2,000 iteraciones

parámetros	q2.5%	Median	q97.5%
intercepto	-33.74242	-25.51390977	-17.59773
beta1	-86.43808	-50.53775106	86.20654
beta2	-56.22651	-3.28926160	48.04959
beta3	-92.80978	98.00417475	124.52621
beta4	-103.00675	-53.78880623	-6.37414
beta5	-80.28676	-28.98926274	77.06557
beta6	-89.04965	38.79923330	90.37534
beta7	-26.02682	-0.06114796	23.77885
beta8	-31.46533	0.49993074	32.48495
beta9	-29.53657	-2.72177658	20.40368
beta10	-36.23520	0.54603412	34.96996
beta11	-20.27582	1.43754123	24.66445
beta12	-31.46700	1.83396840	34.85059
beta13	-98.04408	-1.46568098	99.90742
beta14	-15.73013	10.96349509	42.98066

Los intervalos de confianza revelan mayor información a lo obtenido por la prueba-t, el análisis de incertidumbre revela que parámetros desde beta7 hasta beta14 son no significativos, y otros parámetros como beta1 sus intervalos de confianza son no significativos pero sus densidades muestran que cero no contiene probabilidad.

Este análisis revela que el número de nodos en la base es muy grande, por lo tanto, se deberá probar con un modelo más pequeño. Analizamos los residuos del modelo, el siguiente código muestra están centrados en cero pero con alta dispersión.

summary(m1$residuals)

    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-76.8753 -12.3859  -0.6566   0.0000  12.5556  50.5333 

Finalmente, ajustamos un modelo más pequeño, el modelo M_2 es un modelo con base splines tal que el numero de nodos se estimo con validación cruzada generalizada (GCV), resultando con k = 10 nodos.

m2 = gam(accel ~ s(times),data = mcycle)

pred1 = predict_gam(m1)
pred2 = predict_gam(m2)

pred = rbind(pred1,pred2)
pred$model = sort(rep(c("m1","m2"),50))

ggplot(pred,aes(times, fit))+
  geom_point(data = mcycle,aes(x = times,y = accel))+
  geom_smooth_ci(group = model,ci_alpha = 0.4)+
  labs(title = "Ajuste de los modelos GAMs",
       subtitle = "Accidentes motorizados simulados",
       y = "aceleracion (g)",x  = "tiempo (ms)")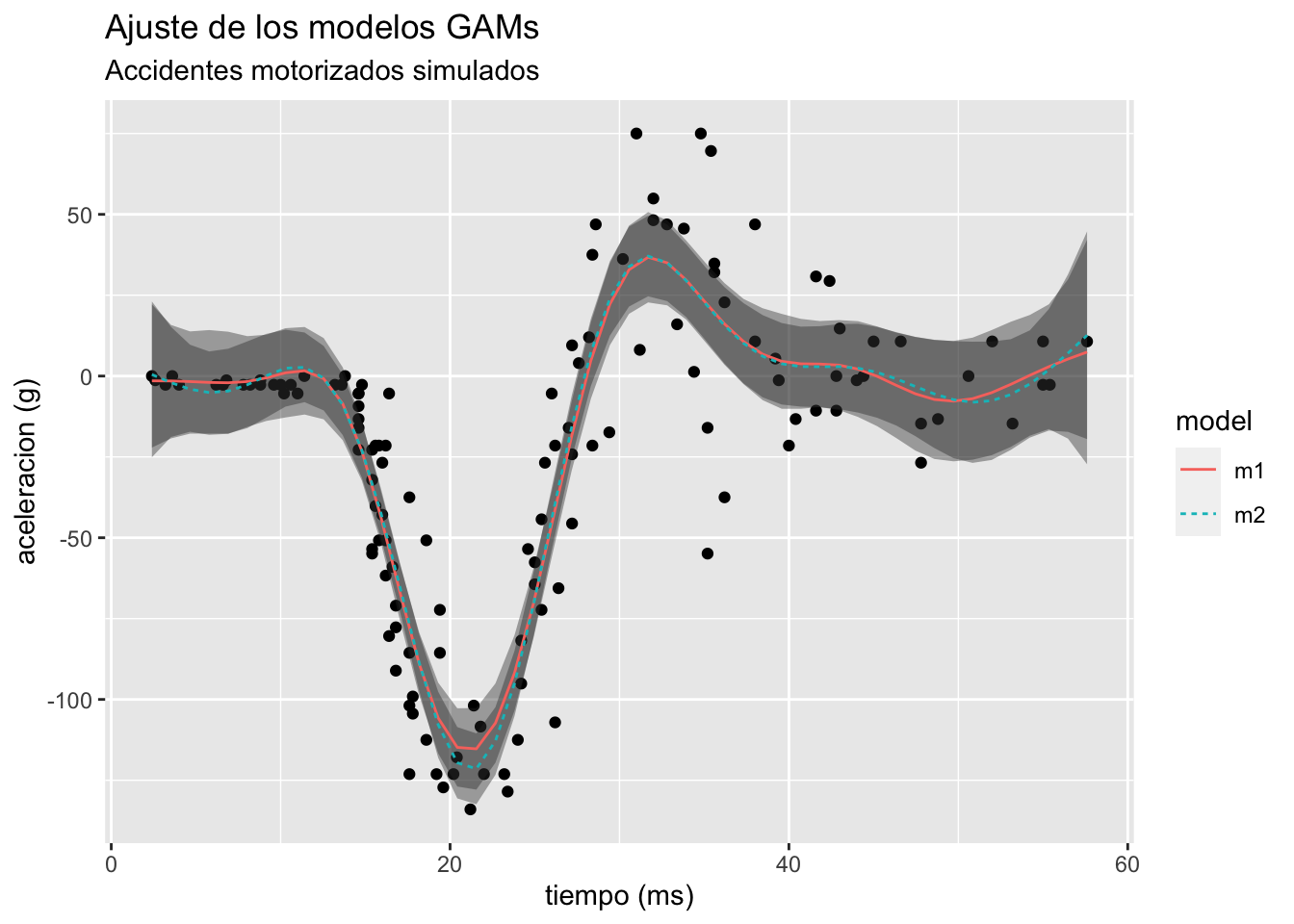

Figure 3: Gráfico de ajuste. Se muestra el ajuste de ambos modelos, estos estiman una curva suave para ambos datos, con la limitante de que los intervalos predictivos no se ajustan a los valores atípicos.

Dado que en este modelo queremos encontrar el mejor ajuste, usar un criterio de información como el AIC es suficiente y necesario. Table 2 compara ambos modelos donde el modelo M_2 que contiene menos nodos presenta un mejor ajuste.

x = AIC(m1,m2)

# Estética
x = data.frame(x)
x$modelo = c("M1","M2")
colnames(x) = c("df","AIC","Modelo")

ft = flextable(x[c(3,1,2)])
autofit(ft)

Table 2: Comparación de modelos bajo el criterio de información de Akaike

Modelo	df	AIC
M1	12.44132	1,220.390
M2	10.69331	1,216.889

Sobrevivencia en el Titanic

Regresamos al análisis de sobrevivencia del Titanic, la base de datos contiene 891 registros y 9 variables, en el trabajo anterior se estimo un modelo GLM logístico para predecir la sobrevivencia de los pasajeros. El modelo seleccionado descartó variables como Fare y Parch, resultando en el modelo:

M2: survival_i \sim \text{Bernoulli}(p_i), \quad p_i = \frac{1}{1 + e^{-\beta X_i}}; y \quad X_i = [Pclass, Sex, Age, SibSp]. El análisis realizado no contempla relaciones no lineales entre Fare y survival. Por lo tanto, re-evaluamos la interacción no lineal con las variables continuas Age y Fare. El nuevo modelo es:

M3: survival \sim \text{Bernoulli}(p_i), \quad p_i = \frac{1}{1 + e^{f_1(X_i)+f_2(X_k)}}. Donde:

• g(p) = \text{logit}(p_i), es la función de enlace.

• g(p) = f_1(X_i) + f_2(X_k). Las covariables interactuan de forma aditiva.

• f_1(X_i) = \beta_1*[Pclass, Sex, SibSp], es un funcional lineal.

• f_2(X_K) = f(Age,Fare) \approx \sum_{k=1}^K \beta_2 b(Age, Fare), es un funcional no lineal.

Ajuste del GAM Logístico

Ajustamos el modelo GAM logístico propuesto,y revisamos el ajuste e inferencia de los parámetros.

m3  = gam(Survived ~ Pclass + Sex + SibSp + s(Fare,Age),
            data = Train, family = "binomial")
summary(m3)

Family: binomial 
Link function: logit 

Formula:
Survived ~ Pclass + Sex + SibSp + s(Fare, Age)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   4.1641     0.5141   8.099 5.53e-16 ***
Pclass       -1.2076     0.2123  -5.689 1.28e-08 ***
Sexmale      -2.6842     0.2261 -11.869  < 2e-16 ***
SibSp        -0.5303     0.1605  -3.305 0.000951 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
              edf Ref.df Chi.sq p-value   
s(Fare,Age) 16.65  21.44  46.34 0.00103 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.437   Deviance explained = 37.7%
UBRE = -0.10016  Scale est. = 1         n = 714

El modelo parece ser adecuado, todos los parámetros son significativos y la interaccion no lineal parece brindar buenos resultados. El siguiente código genera una muestra Bootstrap para cada uno de los parámetros del modelo M_1.

Code

gam_boots = function(dat,B = 2000){
  n = dim(dat)[1]
  est = NULL
  for (i in 1:B) {
    si = sample(x = 1:n,size = n,replace = TRUE)
    mli = gam(Survived[si] ~ Pclass[si] + Sex[si] + SibSp[si] + s(Fare[si],Age[si]),
            data = dat, family = "binomial")
    ci = as.array(mli$coefficients)
    est = rbind(est,ci)
  }
    # Estética
  cn = dim(est)[2]-4
  colnames(est) = c("intercepto","Pclass","Sex","SibSp",paste0("beta",1:cn))
  return(est)
}

Obtenemos una muestra Bootstrap para los estimadores \hat \beta de tamaño B = 2,000 repeticiones.

btp = gam_boots(dat = na.exclude(Train),B = 5000)

color_scheme_set("viridis")

mcmc_dens(btp)+
  labs(title = "Distribución muestral de los estimadores, GAM",
       subtitle ="Bootstrap B = 2,000 iteraciones")

Figure 4: Gráfico de densidades. Cada densidad representa la distribución muestral aproximada para cada uno de los estimadores usando un Bootstrap de B = 2,000 iteraciones.

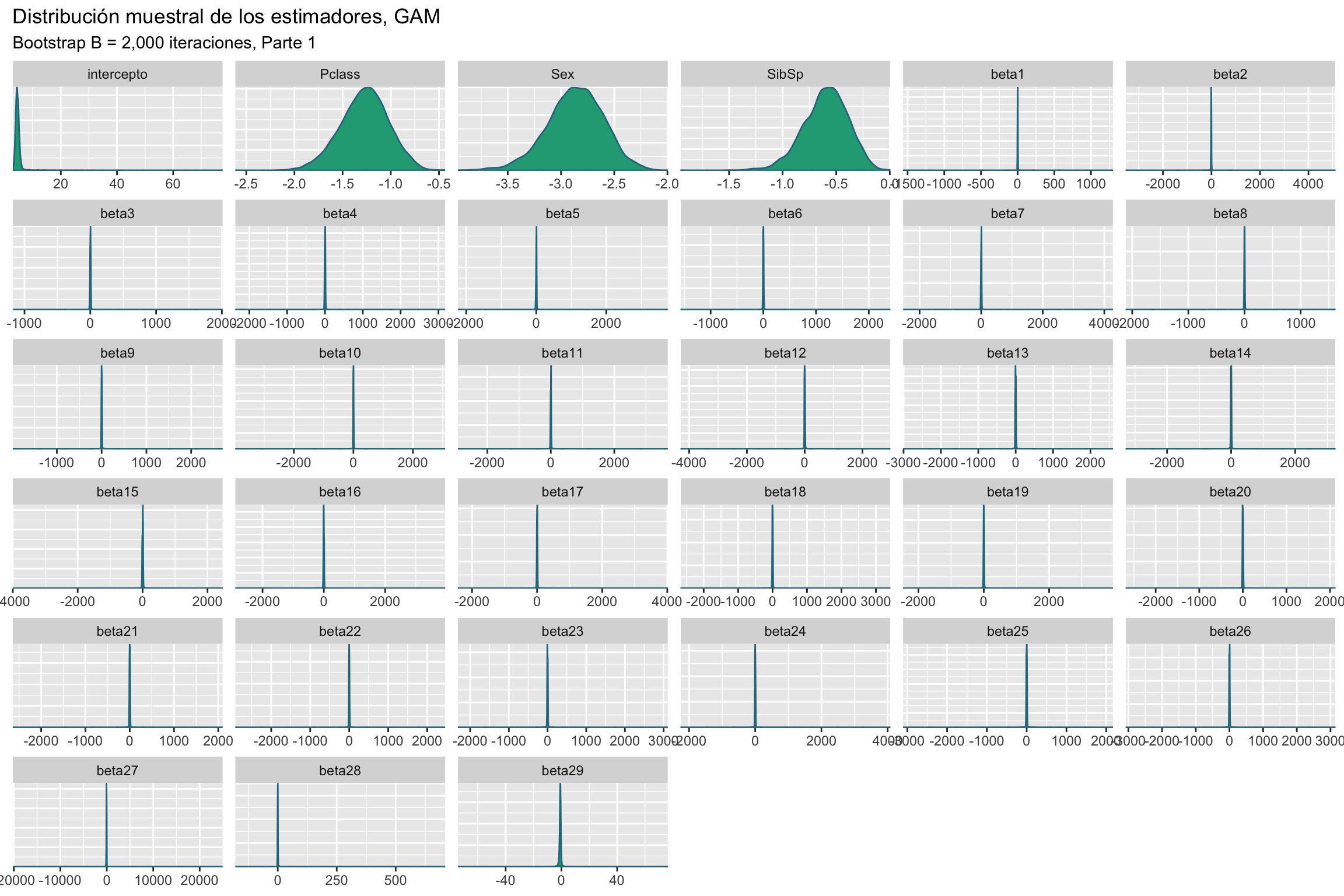
La Figure 2 muestra la distribución muestral de los estimadores del modelo, se observa que los efectos de la componente no lineal son muy dispersos y centrados en cero. Existe la posibilidad que el efecto no lineal sea no significativo.

Para evaluar el ajuste del modelo calculamos la matriz de confusión y la precisión del modelo.

pred1 = predict (m3,Train[,-c(1:2)],type = "response")
pred1 =  ifelse(pred1 > 0.5, 1, 0)
   
x = table(pred1, Train$Survived)
x = round(prop.table(x)*100,2)
x

     
pred1     0     1
    0 51.26 10.50
    1  8.12 30.11

La precisión para el modelo M_3 es:

Accuracy = sum(diag(x))
Accuracy

[1] 81.37

Selección de modelos, 10-fold-CV

Para seleccionar el mejor modelo usaremos validación cruzada, 10-fold, esto implica que ajustaremos diez veces cada modelo, evaluando la precisión del modelo. Los modelos que se consideraran son los siguientes:

• M_2: GLM logístico reducido sin variables Parch y Fare.

• M_3 GAM logístico con variables lineales Pclass, Sex, y SibSp. Componente no lineal Age y Fare

El siguiente código presenta una función para realizar k-fold-CV para cualquier valor de k. En caso de querer añadir otros modelos o criterios, la función deberá ser modificada.

Code

kfold = function(df,k){
  # Generar la particion
  kfld = createFolds(df[,1],k = k)
  mat = NULL
  
  for (i in 1:k) {
    # separar los datos en conjuntos de prueba y entrenamiento
    dfE= df[-kfld[[i]],]
    dfP = df[kfld[[i]],]
    # Ajustar los modelos
    m2  = glm(Survived ~ Pclass + Sex + Age + SibSp,
              data = dfE,family = binomial)
    m3  = gam(Survived ~ Pclass + Sex + SibSp + s(Fare,Age),
            data = dfE, family = "binomial")

    p2 = predict(m2,dfP,type = "response")
    p2 =  ifelse(p2 > 0.5, 1, 0)
    p3  = predict(m3,dfP,type = "response")
    p3 =  ifelse(p3 > 0.5, 1, 0)

    Accuracy = c(
      sum(diag(round(prop.table(table(p2, dfP[,2]))*100,2))),
      sum(diag(round(prop.table(table(p3, dfP[,2]))*100,2)))
    )

    # Unir los datos
    mat = rbind(mat,Accuracy) 
  }
  colnames(mat) = c("Accuracy1","Accuracy2")
  row.names(mat) = NULL
  return(mat)
}

Table 3 presenta los resultados obtenidos al realizar 10-fold-cv, el modelo M_3 es el que presenta la mejor precisión de los dos modelos evaluados.

rst = kfold(df = na.exclude(Train),k = 10)
x = t(apply(rst,MARGIN = 2,FUN = "quantile",probs = c(0.025,0.5,0.975)))

# Estética
x = data.frame(x)
x$pars =  c("Accuracy2", "Accuracy3")
colnames(x) = c("q2.5%","Median","q97.5%","Criterio")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 3: Precisión de los modelos. Mediante Validación cruzada.

Criterio	q2.5%	Median	q97.5%
Accuracy2	72.46450	81.685	87.18725
Accuracy3	72.54325	80.415	87.18725

Referencias

Casella, George, and Roger Berger. 2001. Statistical Inference. Duxbury Resource Center. http://www.amazon.fr/exec/obidos/ASIN/0534243126/citeulike04-21.

DeGroot, M. H., and M. J. Schervish. 2012. Probability and Statistics. Addison-Wesley. https://books.google.es/books?id=4TlEPgAACAAJ.

Gelman, A., J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, and D. B. Rubin. 2013. Bayesian Data Analysis, Third Edition. Chapman & Hall/CRC Texts in Statistical Science. Taylor & Francis. https://books.google.nl/books?id=ZXL6AQAAQBAJ.

Martin, Osvaldo A., Ravin Kumar, and Junpeng Lao. 2021. Bayesian Modeling and Computation in Python. Boca Raton.

Migon, Helio, Dani Gamerman, and Francisco Louzada. 2014. Statistical Inference. An Integrated Approach. Chapman and Hall CRC Texts in Statistical Science. Chapman; Hall.

Roback, paul., and Julie. Legler. 2021. Beyond Multiple Linear Regression: Applied Generalized Linear Models an Multilevel Models in R. Boca Raton.