GLMs Gaussianos: Capacidad de motores de carros

Este post presenta un análisis la base mtcars usando un modelo lineal múltiple con verosimilitud Gaussiana.

La base de datos mtcars contiene el registro de motores de carros mas populares en USA, 1974. los datos contienen 32 registros, con 10 atributos del motor.

library(caret)
library(GGally)
library(ggplot2)
library(flextable)
library(bayesplot)
library(ggfortify)

Se desea predecir la capacidad de consumo de los motores, para eso se evaluaron las siguiente variables.

• mpg: Millas por Galón. (Dependiente)

• hp: Caballos de fuerza.

• carb: número de carburadores.

• wt: peso del motor.

• gears: Número de cambios.

• vs: tipo de motor, recto:1 o tipo V:0.

Verosimilitud

Para medir la relación de consumo de los motores utilizaremos un GLM normal tal que:

mpg_i \sim N(\mu_i,\sigma^2), \quad g(\mu_i) = \mu_i, \text{ y } \mu_i = \beta X_i.

El siguiente código limpia la base de datos para obtener las variables de interés

df = mtcars[,c(1,4,6,8,10,11)]
str(df)

'data.frame':   32 obs. of  6 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Todas las variables son numéricas, pero algunas son totalmente enteras, dificultando el proceso de análisis, se procede a revisar las correlaciones para revisar las interacciones lineales entre variables.

ggpairs(df)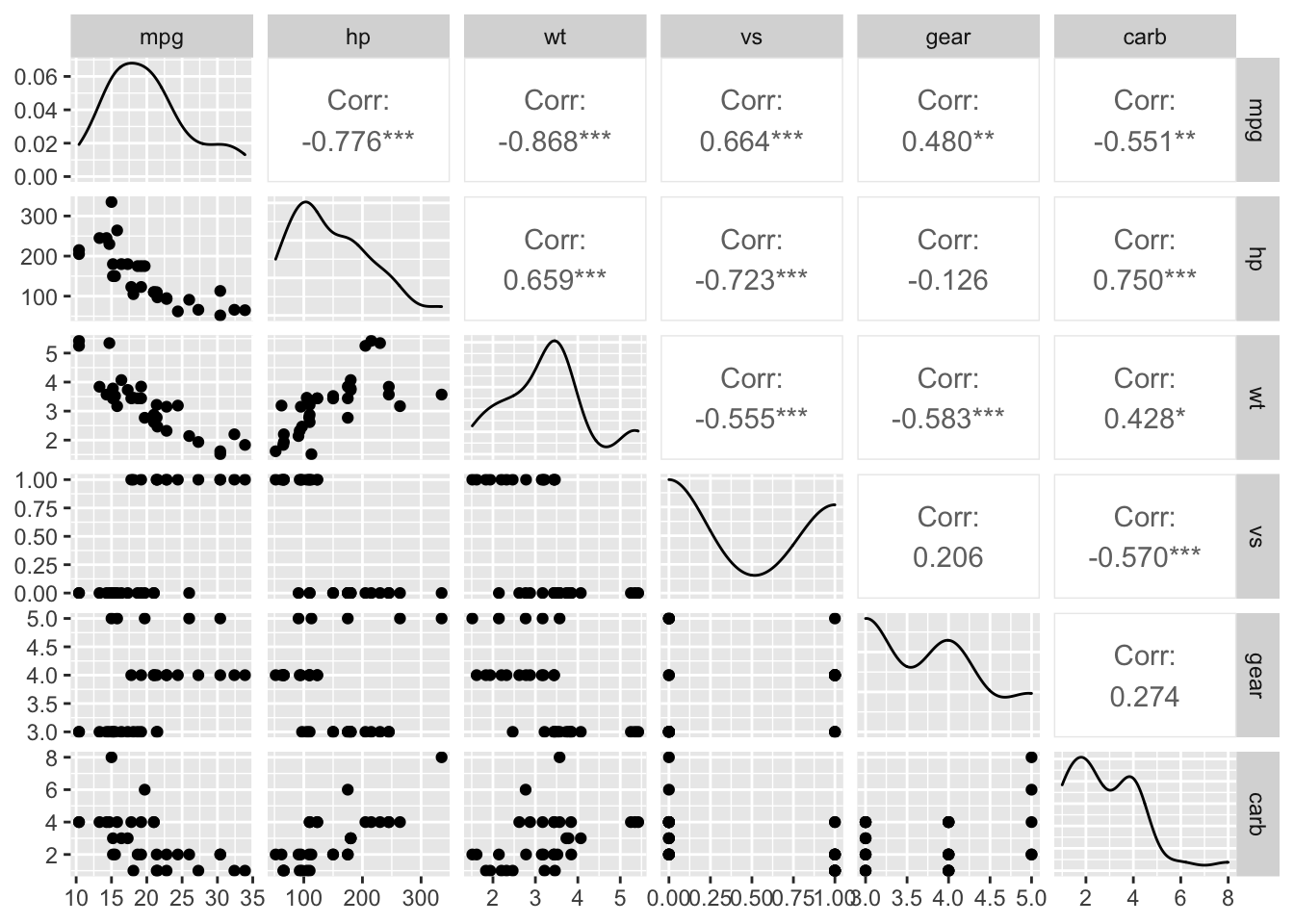

Figure 1: Gráfico de pares. La diagonal principal muestra histogramas densidades de cada una de las variables. La parte superior muestra el coeficiente de correlación entre dos variables, fila y columna. La parte inferior muestra un gráfico de dispersión entre dos variables.

Figure 1 muestra colinealidad entre las variables mpg, hp y wt. Por lo tanto, múltiples modelos deben ser considerados. Realizemos un modelo inicial, el considerado el modelo completo que posee todas las variables

Colinealidad

Dos covariables X_1 y X_2 se dicen ser colineales si las variables son linealmente dependientes.

Recordar que si dos columnas de una matriz son linealmente dependiente, entonces el determinante es cero.

Ajuste del modelo

Ajustamos el modelo completo que consiste en usar todas las variables, y revisamos el ajuste e inferencia de los parámetros.

m1 = lm(mpg~.,data = df)
summary(m1)

Call:
lm(formula = mpg ~ ., data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.2884 -1.4370 -0.3155  1.1697  5.8246 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 27.20311    5.74212   4.737 6.72e-05 ***
hp          -0.02339    0.01353  -1.728   0.0958 .  
wt          -2.74663    0.92005  -2.985   0.0061 ** 
vs           0.94692    1.36929   0.692   0.4954    
gear         1.78520    1.12762   1.583   0.1255    
carb        -0.65498    0.57767  -1.134   0.2672    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.569 on 26 degrees of freedom
Multiple R-squared:  0.8477,    Adjusted R-squared:  0.8184 
F-statistic: 28.94 on 5 and 26 DF,  p-value: 7.653e-10

Debido a la alta colinealidad entre las variables, pocos parámetros estimados son significativos. Procedemos a eliminar algunas variables del modelo. Eliminamos la variable wt al ser colineal con múltiples variables. Por lo tanto, el modelo inicial M_1 es:

m1  =  lm(mpg~vs+hp+gear+carb,data = df)
summary(m1)

Call:
lm(formula = mpg ~ vs + hp + gear + carb, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.8047 -2.3487 -0.0967  1.9188  6.7859 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 13.03756    3.67694   3.546  0.00145 ** 
vs           0.84671    1.55657   0.544  0.59093    
hp          -0.03449    0.01480  -2.331  0.02747 *  
gear         4.20129    0.89285   4.705 6.72e-05 ***
carb        -1.33338    0.60391  -2.208  0.03593 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.921 on 27 degrees of freedom
Multiple R-squared:  0.7955,    Adjusted R-squared:  0.7652 
F-statistic: 26.25 on 4 and 27 DF,  p-value: 5.825e-09

Incertidumbre de los estimadores.

Pese que la función lm de R realiza un análisis de incertidumbre al presentar una Prueba-t de significacia para cada parámetro \beta_i, no presenta los intervalos de confianza. Estos serán estimados con Bootstrap. La siguiente función obtiene una muestra Bootstrap de los parámetros desconocidos \beta.

Code

lm_boots = function(y,x,B = 1000){
  n = length(y)
  est = NULL
  for (i in 1:B) {
    si = sample(x = 1:n,size = n,replace = TRUE)
    mli = lm(y[si]~x[si,] )
    ci = as.array(mli$coefficients)
    est = rbind(est,ci)
  }
  # Estética
  cn = colnames(x)
  colnames(est) = c("intercepto",cn)
  
  return(est)
}

Obtenemos una muestra Bootstrap para los estimadores \hat \beta de tamaño B=5,000 repeticiones

btp = lm_boots(y = df$mpg,x = as.matrix(df[,-1]),B = 5000)

bayesplot_theme_set(theme_grey())
mcmc_dens(btp)+labs(title="Distribución muestral de los estimadores",
                    subtitle ="Bootstrap B = 5,000 iteraciones")

Figure 2: Gráfico de densidades. Cada densidad representa la distribución muestral aproximada para cada uno de los estimadores usando un Bootstrap de B=5,000 iteraciones.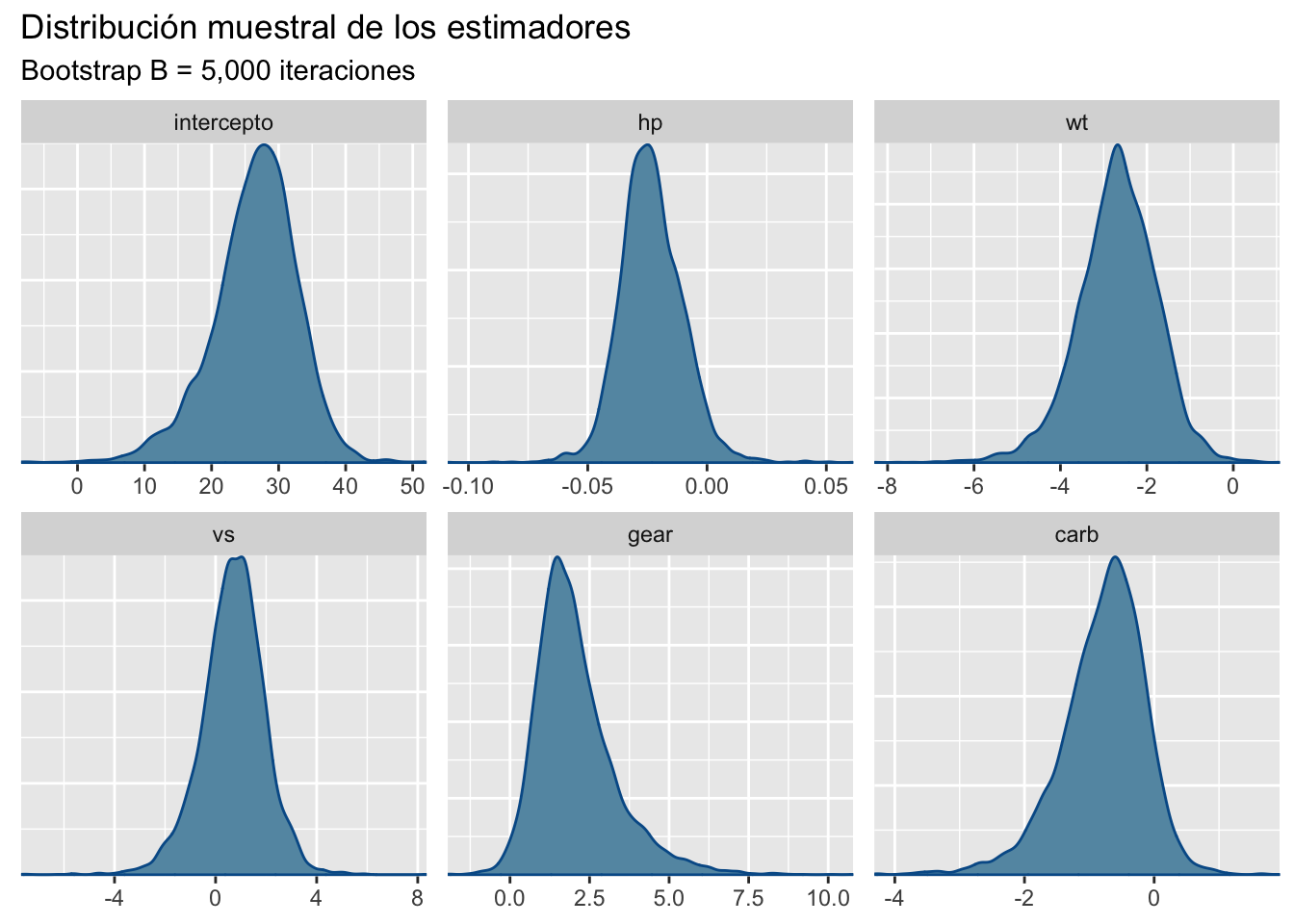

Los intervalos de confianza al 95% son:

x = apply(btp,MARGIN = 2, FUN = quantile, probs = c(0.025,0.5,0.975)) 

# Estética
x = data.frame( t(x) )
x$pars = c("intercepto","hp","wt","vs","gear","carb")
colnames(x) = c("q2.5%","Median","q97.5%","parámetros")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 1: Intervalos de confianza al 95%, obtenidos a partir de una muestra bootstrap de B = 5,000 iteraciones

parámetros	q2.5%	Median	q97.5%
intercepto	11.98569231	26.99019521	37.475629180
hp	-0.04701241	-0.02400519	0.003556438
wt	-4.67879451	-2.66039837	-0.973930849
vs	-1.97116401	0.73672502	3.046150882
gear	0.18837907	1.84889764	5.255645099
carb	-2.27760083	-0.70889865	0.293169770

Los intervalos de confianza revelan mayor información a lo obtenido por la prueba-t, parámetros como hp, y carb que son significativos en la prueba, no lo son mediante los intervalos. Esto indica la posibilidad de un modelo mucho mas reducido.

Análisis de los residuos

Una vez evaluadas las estimaciones del modelo, es necesario revisar los residuos del mismo para corroborar supuestos, la siguiente linea de código presenta un resumen descriptivo de los residuos del modelo inicial M_1, en su mayoría parecen estar centrados en cero.

summary(m1$residuals)

    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-3.80470 -2.34875 -0.09674  0.00000  1.91880  6.78592 

Figure 3 presenta una visualización típica para el diagnostico de los residuos, ninguna figura debe presentar un comportamiento polinómico a excepción del gráfico de quantiles (derecha superior), que debe seguir el comportamiento de una función lineal creciente.

autoplot(m1)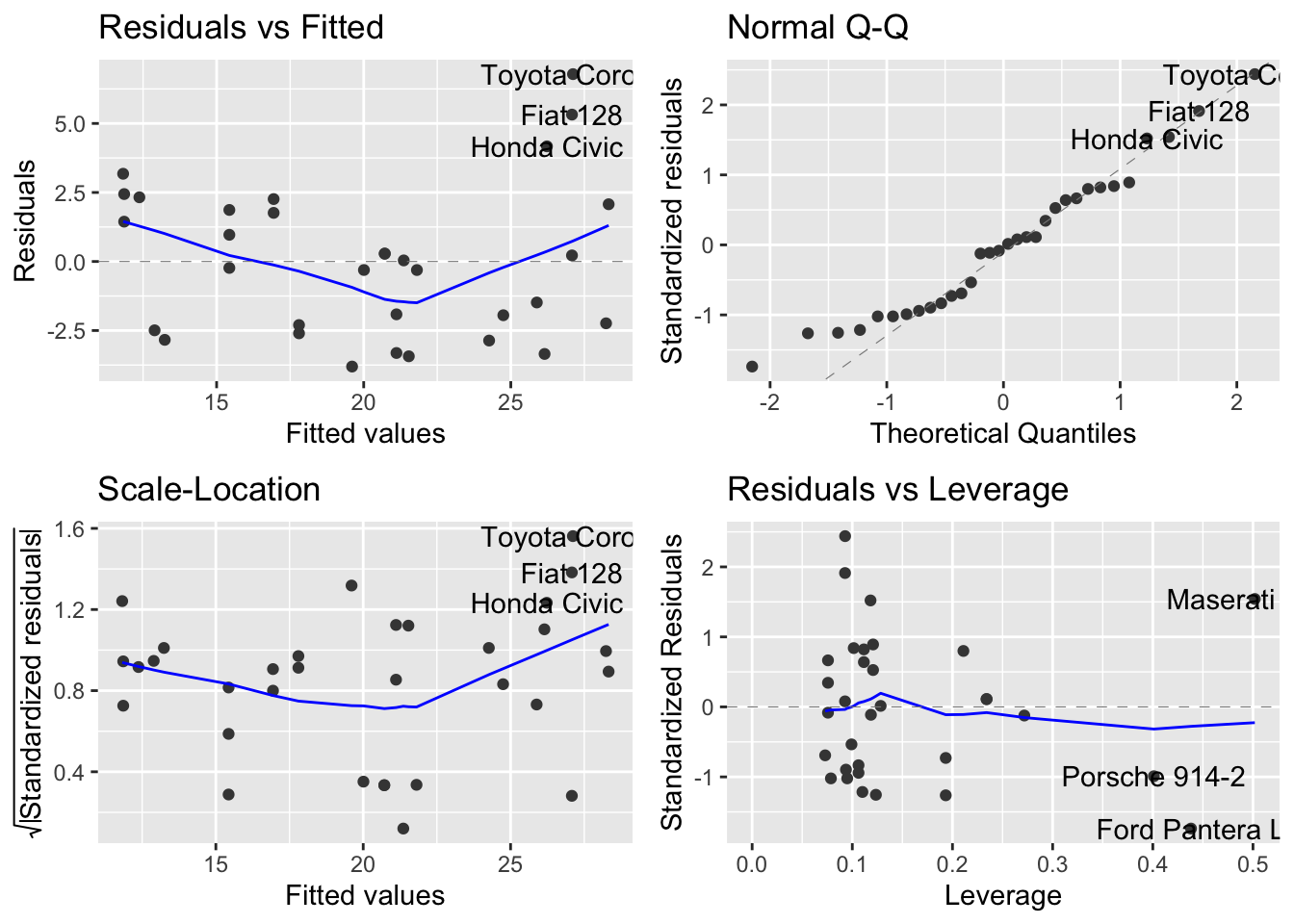

Figure 3: Gráfico diagnóstico de los residuos, estos cuatro gráficos evaluan el ajuste y supuestos del modelo, si algún comportamiento polinómico es persistente, entonces los supuestos del modelo no se satisfacen.

Selección de modelos

Adicional al modelo M_1, ajustamos dos modelos mas:

M_2: \quad mpg \sim N(hp+gear+carb,\sigma^2), M_3: \quad mpg \sim N(wt+gear+carb,\sigma^2).

Code

m2 = lm(mpg~hp+gear+carb,data = df)
m3 = lm(mpg~wt+gear+carb,data = df)

El siguiente código calcula el RMSE de un modelo linea en el conjunto de entrenamiento.

Code

rmse = function(m){
  mse = sum(m$residuals^2)/length(m$residuals)
  return(sqrt(mse))
}

x = matrix(0,nrow = 4,ncol = 3)
x[1,] = c(logLik(m1),logLik(m2),logLik(m3))
x[2,] = c(AIC(m1),AIC(m2),AIC(m3))
x[3,] = c(BIC(m1),BIC(m2),BIC(m3))
x[4,] = c(rmse(m1),rmse(m2),rmse(m3))

# Estética
x = data.frame(x)
x$pars =  c("logLik","AIC","BIC","RMSE")
colnames(x)  = c("Modelo 1","Modelo 2","Modelo 3","Criterio")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 2: Criterios de información de los modelos. Se selecciona el modelo con menores criterios.

Criterio	Modelo 1	Modelo 2	Modelo 3
logLik	-76.986353	-77.160742	-75.196419
AIC	165.972706	164.321484	160.392838
BIC	174.767122	171.650163	167.721517
RMSE	2.682864	2.697525	2.536917

Table 2 muestra la tabla de criterios de información para el conjunto de datos mtcars para sorpresa del lector el mejor modelo es el alternativo M_3 que usa la variable colineal wt en vez de hp.

Validación cruzada

El siguiente código presenta una función para realizar k-fold-CV para cualquier valor de k. En caso de querer añadir otros modelos o criterios, la función deberá ser modificada.

Code

kfold = function(df,k){
  # Generar la particion
  kfld = createFolds(df[,1],k = k)
  mat = NULL
  
  for (i in 1:k) {
    # separar los datos en conjuntos de prueba y entrenamiento
    dfE= df[-kfld[[i]],]
    dfP = df[kfld[[i]],]
    # Ajustar los modelos
    m1 = lm(mpg~vs+hp+gear+carb,data = dfE)
    m2 = lm(mpg~hp+gear+carb,data = dfE)
    m3 = lm(mpg~wt+gear+carb,data = dfE)
    
    p1 = predict(m1,dfP)
    p2 = predict(m2,dfP)
    p3 = predict(m3,dfP)
    
    # Calcular  RMSE
    rmse = c(
             RMSE(pred =  p1,obs = dfP[,1]),
             RMSE(pred =  p2,obs = dfP[,1]),
             RMSE(pred =  p3,obs = dfP[,1])
             )
    # Unir los datos
    mat = rbind(mat,rmse) 
  }
  colnames(mat) = c("RMSE1","RMSE2","RMSE3")
  row.names(mat) = NULL
  return(mat)
}

Table 3 presenta los resultados obtenidos al realizar 5-fold-cv usando el rmse como criterio de información, el modelo M_3 presenta las mejores predicciones. Por lo tanto, M_3 es el modelo con Mayor aprendizaje.

rst = kfold(df = df,k = 5)
x = t(apply(rst,MARGIN = 2,FUN = "quantile",probs = c(0.025,0.5,0.975)))

# Estética
x = data.frame(x)
x$pars =  c("M1","M2","M3")
colnames(x) = c("q2.5%","Median","q97.5%","RMSE")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 3: Criterios de información de los modelos. Mediante Validación cruzada. La tabla presenta los RMSE de cada modelo. bajo un 5-fold cv.

RMSE	q2.5%	Median	q97.5%
M1	2.361410	3.714159	5.988825
M2	2.310997	3.006240	5.520609
M3	2.384538	2.686492	4.825054

Referencias

Casella, George, and Roger Berger. 2001. Statistical Inference. Duxbury Resource Center. http://www.amazon.fr/exec/obidos/ASIN/0534243126/citeulike04-21.

DeGroot, M. H., and M. J. Schervish. 2012. Probability and Statistics. Addison-Wesley. https://books.google.es/books?id=4TlEPgAACAAJ.

Gelman, A., J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, and D. B. Rubin. 2013. Bayesian Data Analysis, Third Edition. Chapman & Hall/CRC Texts in Statistical Science. Taylor & Francis. https://books.google.nl/books?id=ZXL6AQAAQBAJ.

Migon, Helio, Dani Gamerman, and Francisco Louzada. 2014. Statistical Inference. An Integrated Approach. Chapman and Hall CRC Texts in Statistical Science. Chapman; Hall.

Roback, paul., and Julie. Legler. 2021. Beyond Multiple Linear Regression: Applied Generalized Linear Models an Multilevel Models in R. Boca Raton.