Tratamiento para cucarachas

Este post presenta un análisis la base roaches usando un modelo lineal generalizado de conteo.

Se desea establecer la eficacia de cierto pesticida para el reducir el número de cucarachas en apartamentos urbanos. El tratamiento se aplicó a 158 de 262 apartamentos, y es el número de cucarachas atrapadas después de aplicar dicho tratamiento.

library(caret)
library(GGally)
library(ggplot2)
library(rstanarm)
library(flextable)
library(bayesplot)
library(ggfortify)

bayesplot_theme_set(theme_grey())

data(roaches)

Los resultados del estudio se almacenan en la base de datos roaches, que contiene las siguiente variables.

• y: número de cucarachas, después de aplicar el tratamiento. (Dependiente)

• roach1: Número de cucarachas inicial.

• treatment: Indicador de si recibió el tratamiento.

• senior: Indicador si el residente era mayor.

• eposure2: Número de días que se aplicó el tratamiento.

Verosimilitud

La variable y representa el número de cucarachas registradas al finalizar el tratamiento, dicha característica es representada por una v.a. discreta y positiva, y dicha característica debe ser considerada en el modelo.

mcmc_dens(roaches,pars = c("y","roach1"))+
  labs(title = "Gráfico de densidades para el número de cucarachas",
       subtitle = "Pre|Post tratamiento")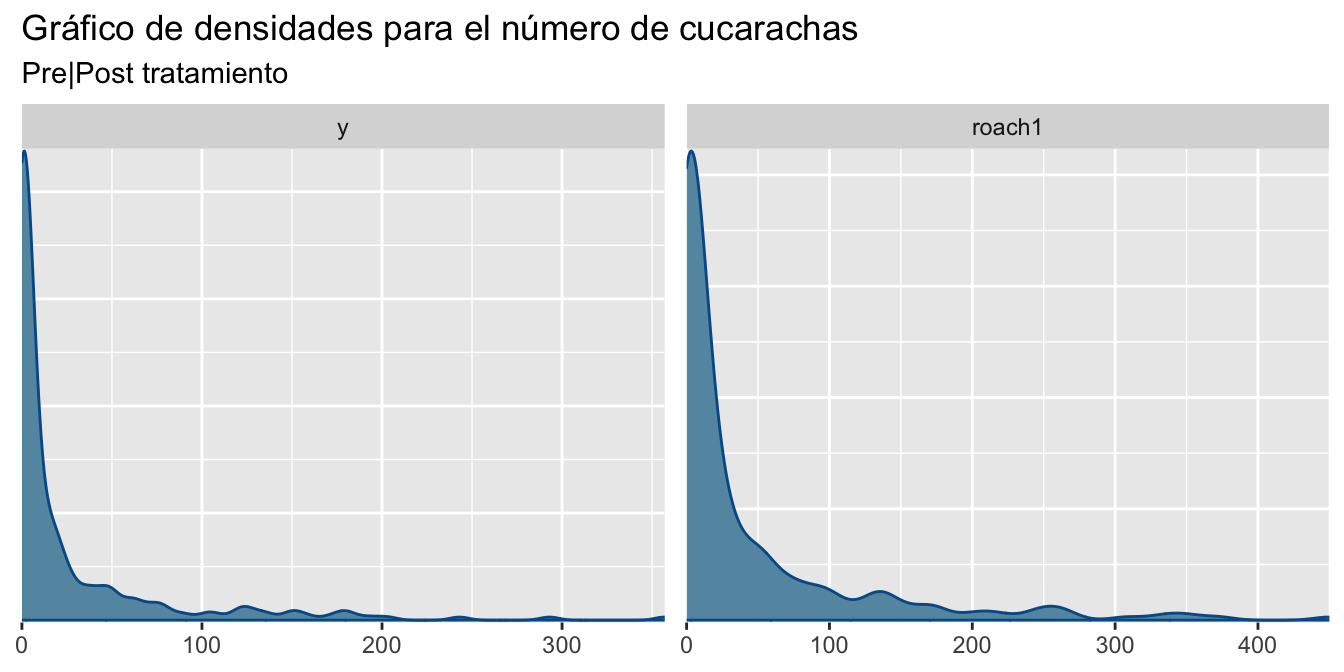

Figure 1: El gráfico izquierdo presenta las densidades de las dos variables de interés, el número de cucarachas previo y post exposición al tratamiento. Ambas variables muestran medias centradas en cero pero con colas bastante pesadas.

Figure 1 muestra que ambas variables y y roach1 son positivas, con colas derechas muy pesadas, para este tipo de datos existen dos alternativas:

• Modelar los datos con una distribución \log N(\mu,\sigma^2).

• Modelar los datos con GLMs de conteo

En GLMs de conteo, la distribución mas popular debido a su simpleza es Poisson pero con una fuerte limitación que los datos poseen media y varianza iguales. Para medir los efectos del tratamiento mediante un GLM de conteo de Poisson definimos la verosimilitud de tal forma que:

y_i \sim \text{Poisson}(\mu_i),\quad g(\mu_i) = \log(\mu_i), \text{ y } \mu_i = \mu_0e^{\beta X_i}. Donde:

• \mu_0 se le conoce como la información previo a la exposición.

• g:\mathbb R \to \mathbb R, es la función de enlace logarítmica g(x) = \log x

• y X son las covariables.

En un modelo log-normal, asumimos que los datos en escala logarítmica siguen un modelo normal

\log y_i\sim N(\mu_i,\sigma^2), \quad g(\mu_i) = \mu_i, \text{ y } \mu_i = \beta X_i. Es importante tener en cuenta que la función logarítmica es convexa, por ende no se puede aplicar la transformación inversa para obtener las predicciones en las escalas originales. Recordar que si y \sim \log N(\mu,\sigma^2) entonces:

E[y] = e^{\mu +1/2\sigma}. Finalmente realizamos un gráfico de correlaciones para identificar las interacciones lineales entre variables.

ggpairs(roaches )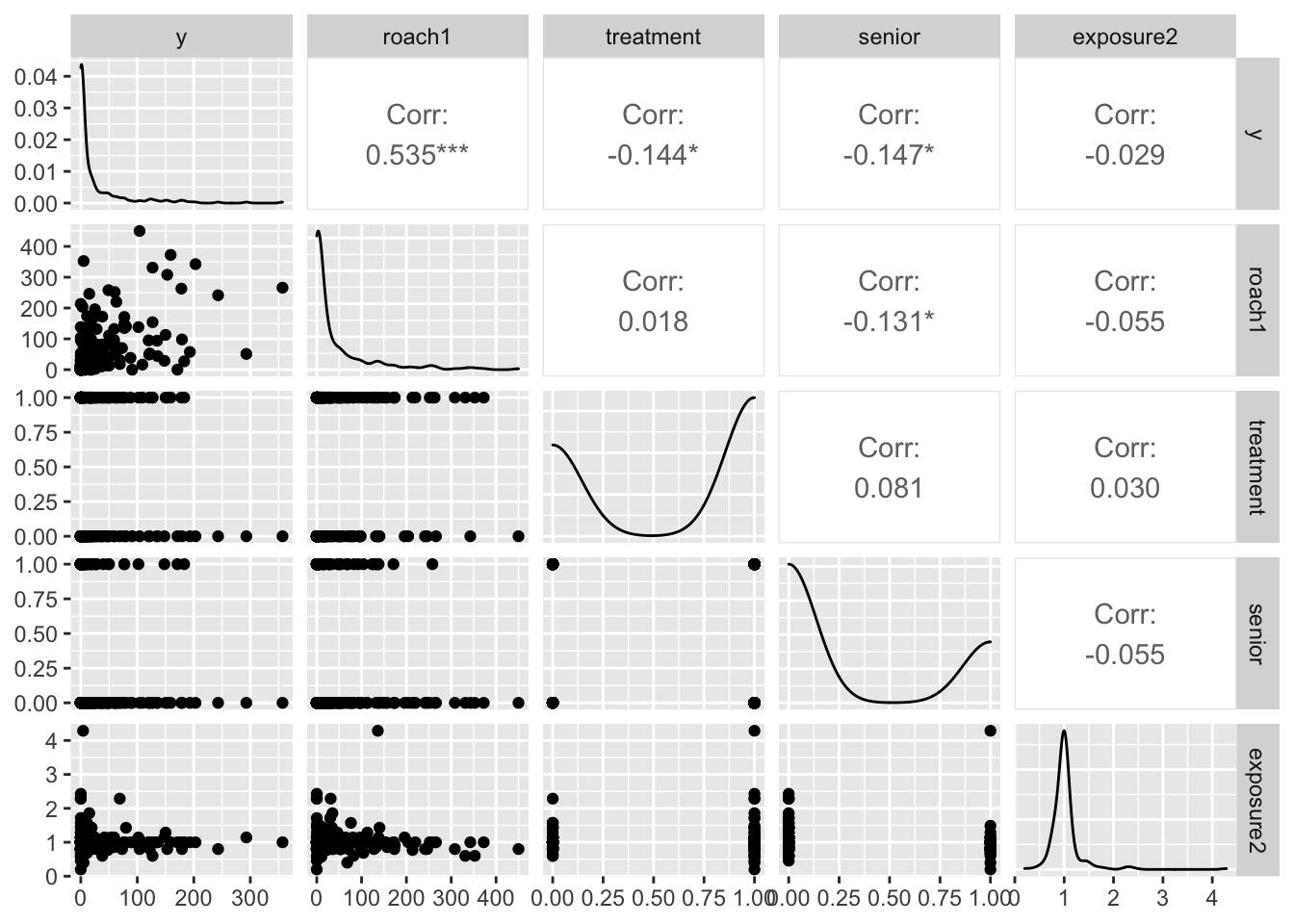

Figure 2: Gráfico de pares. La diagonal principal muestra histogramas densidades de cada una de las variables. La parte superior muestra el coeficiente de correlación entre dos variables, fila y columna. La parte inferior muestra un gráfico de dispersión entre dos variables.

Figure 2 muestra resultados anti-intuitivos, se esperaría una alta correlación entre las variables y y roach1, dado que ambas miden la misma información pero en tiempos diferentes. Dado la poca correlación entre las variables consideramos un modelo completo que incluya todas las interacciones en el modelo.

Ajuste del modelo de Conteo de Poisson

Ajustamos el modelo GLM de conteo completo que consiste en usar todas las variables, y revisamos el ajuste e inferencia de los parámetros.

m1  = glm(y ~ roach1 + treatment + senior, offset = log(exposure2),
            data = roaches, family = poisson)

summary(m1)

Call:
glm(formula = y ~ roach1 + treatment + senior, family = poisson, 
    data = roaches, offset = log(exposure2))

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-17.9430   -5.1529   -3.8059    0.1452   26.7771  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)  3.089e+00  2.123e-02  145.49   <2e-16 ***
roach1       6.983e-03  8.874e-05   78.69   <2e-16 ***
treatment   -5.167e-01  2.474e-02  -20.89   <2e-16 ***
senior      -3.799e-01  3.342e-02  -11.37   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 16954  on 261  degrees of freedom
Residual deviance: 11429  on 258  degrees of freedom
AIC: 12192

Number of Fisher Scoring iterations: 6

El modelo completo da una impresión con buenos resultados, todas las variables son significativas pero los residuos no están centrados en cero, por ende no cumplen los supuestos iniciales. El siguiente código genera una muestra Bootstrap para los parámetros del modelo M_1.

Code

glm_boots = function(y,x,exposure,B = 1000){
  n = length(y)
  est = NULL
  for (i in 1:B) {
    si = sample(x = 1:n,size = n,replace = TRUE)
    mli = glm(y[si]~x[si,], offset = log(exposure[si]),family = poisson)
    ci = as.array(mli$coefficients)
    est = rbind(est,ci)
  }
  # Estética
  cn = colnames(x)
  colnames(est) = c("intercepto",cn)
  
  return(est)
}

Obtenemos una muestra Bootstrap para los estimadores \hat \beta de tamaño B = 2,000 repeticiones

btp = glm_boots(y = roaches$y,
               x = as.matrix(roaches[,2:4]),
               exposure = roaches$exposure2,B = 2000)

color_scheme_set("green")
mcmc_dens(btp)+labs(title="Distribución muestral de los estimadores, GLM Poisson",
                    subtitle ="Bootstrap B = 2,000 iteraciones")

Figure 3: Gráfico de densidades. Cada densidad representa la distribución muestral aproximada para cada uno de los estimadores usando un Bootstrap de B = 2,000 iteraciones.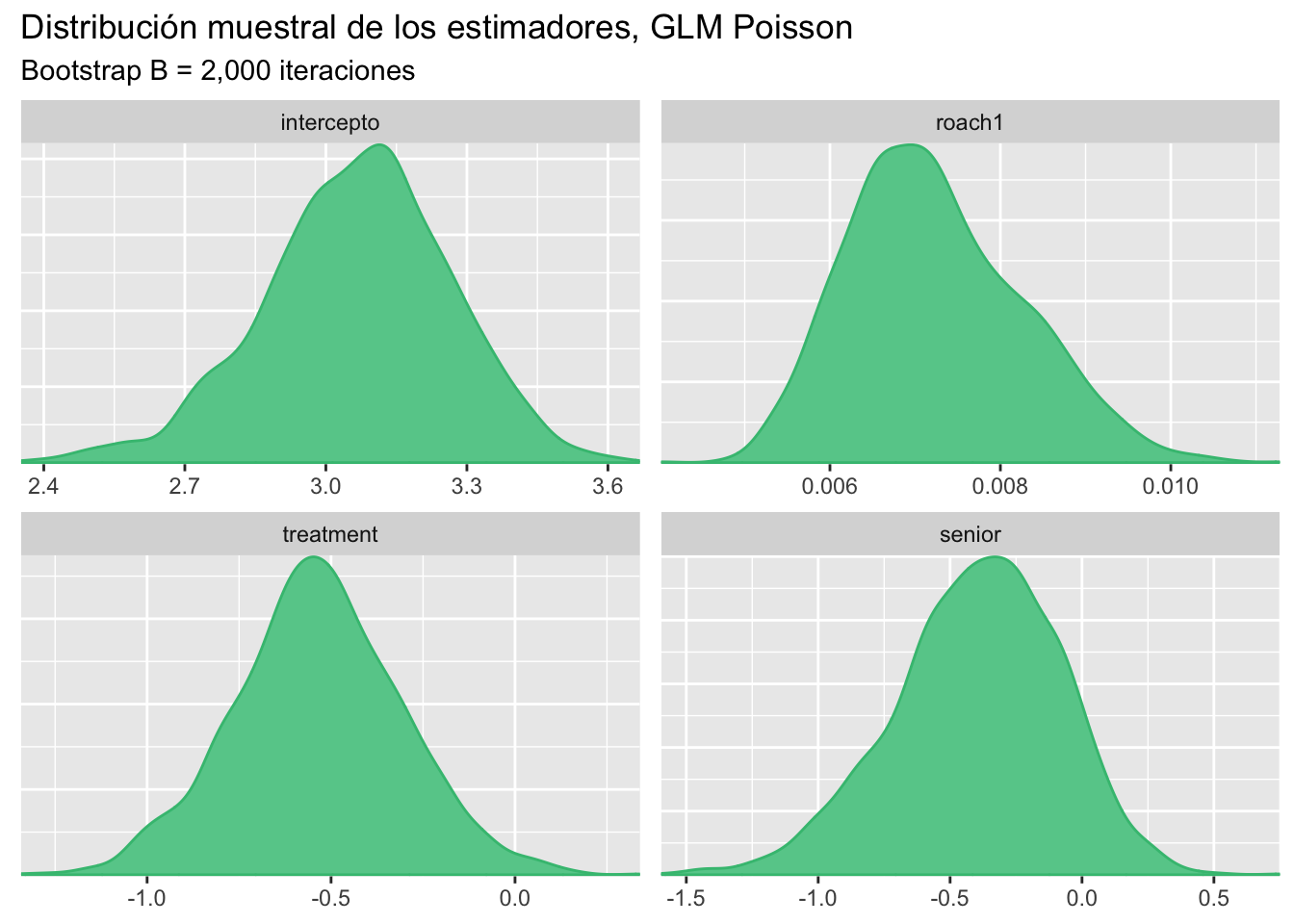

Los intervalos de confianza al 95% son:

x = apply(btp,MARGIN = 2, FUN = quantile, probs = c(0.025,0.5,0.975)) 

# Estética
x = data.frame( t(x) )
x$pars = c("intercepto","roach1","treatment","senior")
colnames(x) = c("q2.5%","Median","q97.5%","parámetros")

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 1: Intervalos de confianza al 95%, obtenidos a partir de una muestra bootstrap de B = 2,000 iteraciones

parámetros	q2.5%	Median	q97.5%
intercepto	2.644649555	3.074843284	3.435461027
roach1	0.005482779	0.007119675	0.009384559
treatment	-0.989904660	-0.537908236	-0.075859077
senior	-1.053324226	-0.376491503	0.165152478

Los intervalos de confianza muestran que el efecto de la variable roach1 esta concentrado en cero, por lo tanto, se deberá considerar un GLM de Poisson excluyendo dicha variable.

Ajuste del modelo log-normal

Ajustamos el modelo GLM log-normal completo que consiste en usar todas las variables, y revisamos el ajuste e inferencia de los parámetros. Hay que tomar en cuenta que al tomar y y roach1 en escala logarítmica, se tendrán que descartar los valores infinitos obtenidos, dado que las distribuciones se acumulan en cero

df = roaches
df[,1:2] = log(df[,1:2])
df = subset(df,subset = df$y != -Inf & df$roach1 != -Inf)

m2 = lm(y~.,data = df)
summary(m2)

Call:
lm(formula = y ~ ., data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.0679 -1.0726  0.2976  0.9884  2.8697 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.58442    0.40132   3.948 0.000122 ***
roach1       0.52136    0.06408   8.137 1.62e-13 ***
treatment   -0.38609    0.21808  -1.770 0.078746 .  
senior      -0.38632    0.25848  -1.495 0.137187    
exposure2   -0.19054    0.30949  -0.616 0.539082    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.299 on 146 degrees of freedom
Multiple R-squared:  0.3315,    Adjusted R-squared:  0.3132 
F-statistic:  18.1 on 4 and 146 DF,  p-value: 4.281e-12

El modelo completo da una mala impresión,hay variables no significativas, el coeficiente de determinación \hat R = 0.31 es bastante cercano a cero, y los residuos no están centrados en cero, por ende no cumplen los supuestos iniciales. Finalmente, revisamos los residuos del modelo, dado que los supuestos de normalidad pueden ser evaluados.

autoplot(m2)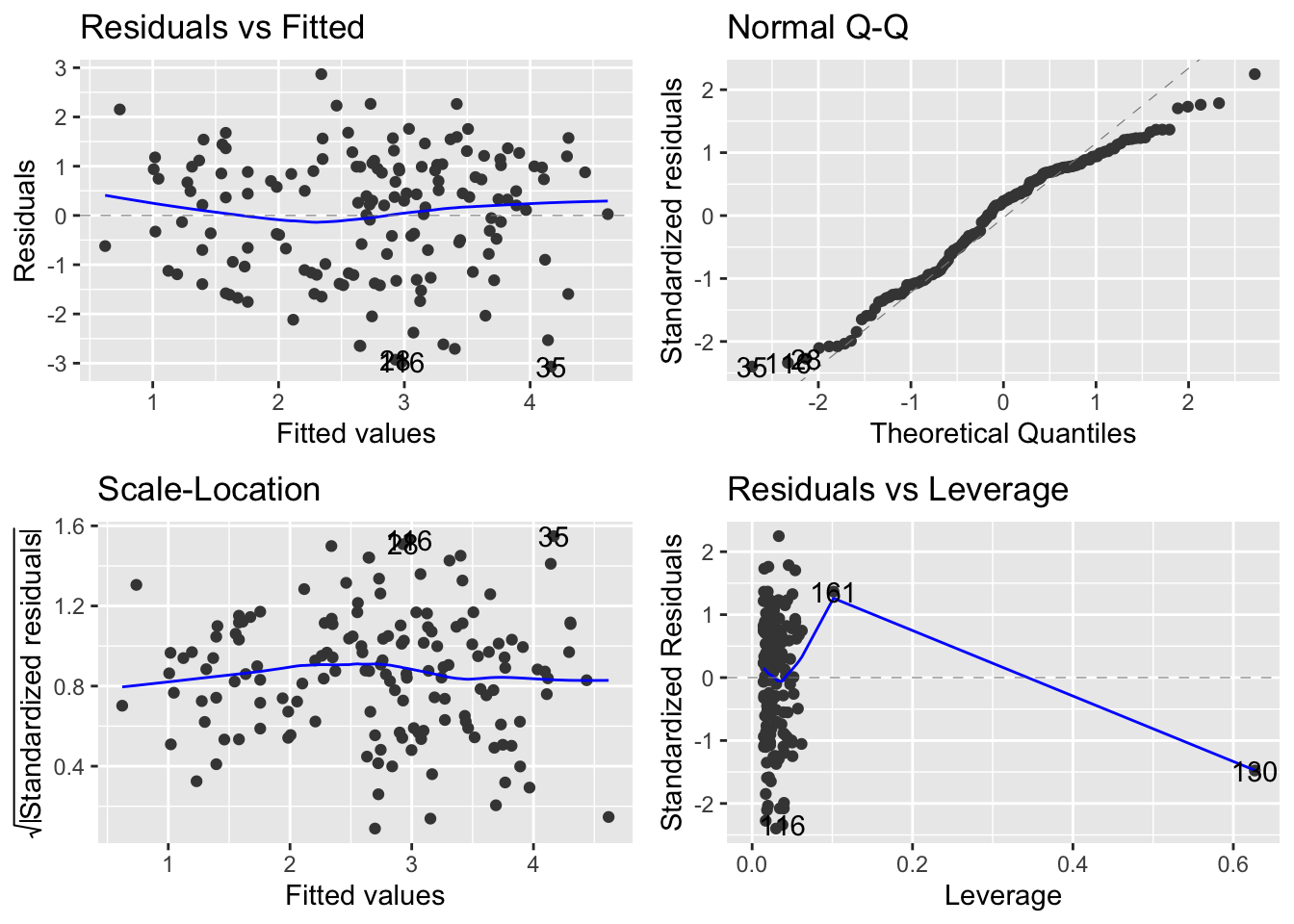

Figure 4: Gráfico diagnóstico de los residuos, estos cuatro gráficos evaluan el ajuste y supuestos del modelo, si algún comportamiento polinómico es persistente, entonces los supuestos del modelo no se satisfacen.

Figure 4 muestra que los supuestos de normalidad en su mayoría si se cumplen, el gráfico inferior izquierdo muestra un comportamiento irregular, pero debido a que una observación es anómala e influenciable, por lo tanto, otro modelo a considerar es usando una distribución Student-t con grados de libertad cercanos a v = 3.

Modelo de Conteo, Binomial Negativa

La distribución Binomial negativa mide el número de éxitos que ocurren hasta el k-ésimo fracaso. Una v.a.d se distribuye Binomial Negativa (y_i \sim BN(k,p)) si:

f(y|p) = \binom{y+k-1}{y}(1-p)^k p^y.

Donde:

• p es la probabilidad de éxito de un experimento Bernoulli.

• k es el número de fracasos hasta tener el primer éxito

• E[y_i] = \frac{pk}{1-p} es el valor esperado.

• V[y_i] = \frac{pk}{(1-p)^2}, es la varianza.

Esta distribución se puede re-parametrizar en términos de su media E[y_i] = \mu y varianza V[y] = \sigma^2.

• p = \frac{\sigma^2 - \mu}{\sigma^2},

• k = \frac{\mu^2}{\sigma^2 - \mu}.

f(y) = \binom{y+\frac{\mu^2}{\sigma^2 - \mu}-1}{y}\left(\frac{\sigma^2 - \mu}{\sigma^2}\right)^y \left(\frac{\mu}{\sigma^2}\right)^{\frac{\mu^2}{\sigma^2 - \mu}}

Para medir los efectos del tratamiento mediante un GLM de conteo de Binomial negativa, definimos la verosimilitud de tal forma que:

y_i \sim BN(\mu_i,\sigma^2)\quad g(\mu_i) = \log(\mu_i), \text{ y } \mu_i = \mu_0e^{\beta X_i}.

Donde:

• \mu_0 se le conoce como la información previo a la exposición.

• g:\mathbb R \to \mathbb R, es la función de enlace logarítmica g(x) = \log x

• y X son las covariables.

• El modelo no tiene la limitante que la varianza es la media V[y_i] \neq \mu_i.

Ajustamos el modelo GLM de conteo completo que consiste en usar todas las variables, y revisamos el ajuste e inferencia de los parámetros.

library(MASS)

m3 = glm.nb(y ~ roach1 + treatment + senior + exposure2,data = roaches)
summary(m3)

Call:
glm.nb(formula = y ~ roach1 + treatment + senior + exposure2, 
    data = roaches, init.theta = 0.2717608411, link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.8052  -1.3452  -0.6815  -0.0344   3.1831  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.393790   0.441811   5.418 6.02e-08 ***
roach1       0.012764   0.001601   7.975 1.52e-15 ***
treatment   -0.764550   0.245659  -3.112  0.00186 ** 
senior      -0.341062   0.264555  -1.289  0.19733    
exposure2    0.435159   0.374132   1.163  0.24478    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(0.2718) family taken to be 1)

    Null deviance: 338.89  on 261  degrees of freedom
Residual deviance: 277.87  on 257  degrees of freedom
AIC: 1792.7

Number of Fisher Scoring iterations: 1

              Theta:  0.2718 
          Std. Err.:  0.0259 

 2 x log-likelihood:  -1780.7380 

El modelo completo presenta mejores resultados que el modelo de Poisson pese que no todas las variables son significativas. Los residuos están centrados en cero y menos disperso, cumpliendo los supuestos iniciales.

Selección de modelos, 5-fold CV

Para seleccionar el mejor modelo usaremos validación cruzada, 5-fold, esto implica que ajustaremos cinco veces cada modelo, evaluando la capacidad de aprendizaje usando AIC, RMSE y MAE. Los modelos que se consideraran son los siguientes:

• M_1: Modelo de Poisson completo

• M_2: Modelo log-normal completo.

• M_3: Modelo Binomial Negativa completo.

• M_{3.1}: Modelo BN reducido, sin la variable roach1.

El siguiente código presenta una función para realizar k-fold-CV para cualquier valor de k. En caso de querer añadir otros modelos o criterios, la función deberá ser modificada.

Code

kfold = function(df,k){
  # Generar la particion
  kfld = createFolds(df[,1],k = k)
  mat = NULL
  
  for (i in 1:k) {
    # separar los datos en conjuntos de prueba y entrenamiento
    dfE= df[-kfld[[i]],]
    dfP = df[kfld[[i]],]
    # Ajustar los modelos
    m1  = glm(y ~ roach1 + treatment + senior, offset = log(exposure2),
            data = dfE, family = poisson)
    m3  = glm.nb(y ~ roach1 + treatment + senior + exposure2,data = roaches)
    m31 =  glm.nb(y ~ treatment + senior + exposure2,data = roaches)
    
    p1  = predict(m1,dfP)
    p3  = predict(m3,dfP)
    p31 = predict(m31,dfP)
    
    # Calcular MAE
    mae = c(
             MAE(pred =  p1,obs = dfP[,1]),
             MAE(pred =  p3,obs = dfP[,1]),
             MAE(pred =  p31,obs = dfP[,1])
            )

    # Unir los datos
    mat = rbind(mat,mae) 
  }
  colnames(mat) = c("MAE1","MAE3","MAE31")
  row.names(mat) = NULL
  return(mat)
}

kfold1 = function(df,k){
  # Generar la particion
  kfld = createFolds(df[,1],k = k)
  mat = NULL
  
  for (i in 1:k) {
    # separar los datos en conjuntos de prueba y entrenamiento
    dfE= df[-kfld[[i]],]
    dfP = df[kfld[[i]],]
    # Ajustar los modelos
    m2 = lm(y ~ .,data = dfE)
    p2  = predict(m2,dfP)

    # Unir los datos
    mat = rbind(mat,MAE(pred =  p2,obs = dfP[,1])) 
  }
  colnames(mat) = c("MAE2")
  row.names(mat) = NULL
  return(mat)
}

Table 2 compara los modelos de conteo, se observa que en la mayoría de criterios el modelo Binomial Negativa completo, presenta los mejores resultados y el mejor ajuste, por lo tanto, seleccionamos al modelo M_3 que este deberá ser comparado con el modelo log-normal.

Code

rst = kfold(df = roaches,k = 5)
x = t(apply(rst,MARGIN = 2,FUN = "quantile",probs = c(0.025,0.5,0.975)))

# Estética
x = data.frame(x)
x$pars =  c("M1","M3","M3.1")

colnames(x) = c("q2.5%","Median","q97.5%","MAE")

rst1 = kfold1(df = df,k = 5)
x1 = t(apply(rst1,MARGIN = 2,FUN = "quantile",probs = c(0.025,0.5,0.975)))

# Estética
x1 = data.frame(x1)
x1$pars = c("M2")
colnames(x1) = c("q2.5%","Median","q97.5%","MAE")

x = rbind(x,x1)

ft = flextable(x[c(4,1,2,3)])
autofit(ft)

Table 2: Criterios de información del modelo log-N. Mediante Validación cruzada. La tabla presenta los criterios AIC, RMSE, y MAE bajo un 5-fold cv.

MAE	q2.5%	Median	q97.5%
M1	19.760629	23.350825	35.08891
M3	19.687457	23.170492	34.81726
M3.1	19.783609	23.537866	35.42434
M2	0.977912	1.042327	1.26739

Contrario a los esperado, el modelo log-normal M_2 presenta mejores resultados que los modelos de conteos, por lo tanto el mejor modelo para medir el efecto de tratamientos en cucarachas desde un enfoque de aprendizaje es el modelo log-normal.

Es importante resaltar que las predicciones realizadas con el modelo M_2 se realizaron en escala logarítmica,

RMSE = \frac{1}{\sqrt n}||\hat{\log (y_P)} -\log (y_P)||_2. Es necesario revisar si al transformar de forma inversa el modelo mantiene las predicciones. En caso de evaluar las predicciones en la escala natural de los datos, corroborar si:

RMSE = \frac{1}{\sqrt n}||e^{\mu_p+0.5\sigma} -y_P||_2. Donde \mu_P son las predicciones obtenidas del modelo en escala logarítmica.

Referencias

Casella, George, and Roger Berger. 2001. Statistical Inference. Duxbury Resource Center. http://www.amazon.fr/exec/obidos/ASIN/0534243126/citeulike04-21.

DeGroot, M. H., and M. J. Schervish. 2012. Probability and Statistics. Addison-Wesley. https://books.google.es/books?id=4TlEPgAACAAJ.

Gelman, A., J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, and D. B. Rubin. 2013. Bayesian Data Analysis, Third Edition. Chapman & Hall/CRC Texts in Statistical Science. Taylor & Francis. https://books.google.nl/books?id=ZXL6AQAAQBAJ.

Migon, Helio, Dani Gamerman, and Francisco Louzada. 2014. Statistical Inference. An Integrated Approach. Chapman and Hall CRC Texts in Statistical Science. Chapman; Hall.

Roback, paul., and Julie. Legler. 2021. Beyond Multiple Linear Regression: Applied Generalized Linear Models an Multilevel Models in R. Boca Raton.